聚苯乙烯颗粒的稀相气力输送系统
发布时间:2018-08-07 15:20 | 作者: 气力输送 | 来源: 未知
聚苯乙烯颗粒的稀相气力输送系统:管道横截面上的压降曲线和颗粒分布
在塑料粒料的气力输送过程中,已经观察到具有相似物理特性的材料可能在压降方面产生显着差异。 在这项工作中,从实验角度展示了具有圆形横截面的载有颗粒的2.7米长水平通道中的压降。 对圆柱形聚苯乙烯珠粒进行实验,平均直径为3.2mm,质量载荷为0.06-0.11(kg颗粒/ kg气体)。 研究了空气质量流量在0.085kg / s至0.170kg / s的范围内。 压降曲线显示为空气速度和颗粒载荷的函数。 响应面法对空气速度,粒子载荷及其交叉关系表现出高度统计学意义。
关键词:气力输送系统; 颗粒状固体; 聚苯乙烯; 粒子分布; 压力损失。
输送管道中的固体流动通常通过应用两种不同的流动技术进行:密相和稀相。 在致密相中,施加高浓度的固体,通常大于30%v / v,速度为1-5m / s。 密相状态具有高的采集,操作和维护成本,因为它需要高气压(压力高于20 mbar / m)。 稀相输送在低于1%v / v的固体浓度和高于20m / s的速度下运行。 稀相方案成本较低,但在低运输速度下会引起不规则的管道磨损,主要是在水平管道的下部。
在稀相中气动输送系统的性能受压降的影响很大,而压降又取决于几个参数,例如材料特性,管道设计和气流。
本研究的目的是获得圆柱形聚苯乙烯颗粒的压降曲线,并分析空气速度和固体载荷对压降的影响。 响应面法用于分析空气速度和固体载荷对压降响应的影响。
实验装置的圆柱形通道的总长度为4.2米。 通道的第一部分长1.5米,用于在聚合物颗粒的进料点之前获得完全发展的气流。 圆柱形通道的初始部分具有流量调节器,其位于鼓风机后0.9m处,其用于使管流中的速度分布均匀化。 流量调节器还旨在加速形成完全发展的湍流速度分布,其在调节器下游约25个直径处获得(Xiong等人,2005)。
实验装置的主要部件由圆柱形通道组成,放置在颗粒的进料点之后,长2.7米,内径117毫米。 这种配置允许建立二维流动条件,其中由于颗粒沉降,重力破坏了两相流中的圆柱对称( 图1和2 )。
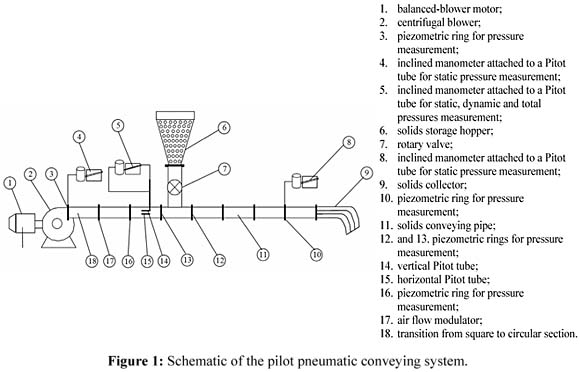

通过离心式鼓风机(引持环保)引入空气,其具有100mm直径的半开式叶片,203mm直径的吸入管线和102mm方形排出部分,其连接至1Hp可变旋转马达,其中两个额外的轴承是增加(平衡鼓风机马达)来评估机械功率。
通过皮托管测量总压力和静压。 这些管由两根190mm长的“L”形同轴管组成。 内管的内径为3毫米,外管的内径为8毫米,按照ASME规范制造。 总压力通过皮托管的中心管获得,而静压通过放置在皮托管外管壁中的小孔获得。 动态压力确定为总压力和静压力之间的差值。 皮托管放置在第一个测压环后0.13米处和流量调节器后0.53米处。
在流动调节器之后,分别将第一,第二,第三和第四测压环放置在0.40米,0.60米,1.20米和3.00米处。
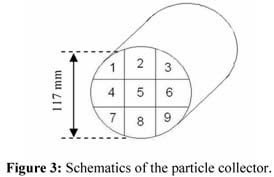
借助于带有六个径向叶片的旋转阀将固体从进料容器送入输送管,测量为92mm×42mm,直径为76.2mm。 将固体排放到位于水平气动输送机末端的收集器模块中。 颗粒分布分析模块由九个方形截面的铝管组成,尼龙袋连接在其上以收集固体颗粒( 图3 )。 负载 μ (固体质量流量/空气质量流量)由气流阀和旋转阀的相互作用控制。
在测试中使用聚苯乙烯颗粒(PS)并由BASF提供。 聚苯乙烯颗粒的性质列于表1中 。

通过将固体质量流速设定为0.085kg / s,0.13kg / s和0.17kg / s(此处分别称为G 1 ,G 2和G 3 )来建立作为空气速度的函数的聚苯乙烯压降特性曲线。 。 速度从5到35米/秒变化,载体上的压力用连接到倾斜压力计的测压环测量。 在这些条件下的最小和最大颗粒负载量分别为0.5kg颗粒/ kg空气和7.8kg颗粒/ kg空气。
聚苯乙烯在管道中的分布是根据安装在输送管末端的九管收集模块中的固体质量确定的; 管道编号如图3所示。 在每个袋中收集的质量用于计算每单位面积的质量分数,然后允许计算聚苯乙烯在管的横截面中对于所有空气速度和固体质量流速的分散。
计算九个收集器的颗粒密度,并且还使用表面响应方法处理这些点。 使用软件Statistica v7.0基于使用距离加权最小二乘法的数据内插来生成粒子分布轮廓。 应用该方法是因为它为非对称轮廓提供了更好的数据拟合。
将水平和垂直方向上的压降测量值归一化为 ΔP/ L,其中L是压力抽头之间的距离。 图4显示了聚苯乙烯颗粒在水平方向上的压降与载荷和空气速度的关系。 图4中的A'B'部分表示由整个水平传输线中的空气流(无固体流速G 0 = 0)引起的压降。 由于内部摩擦,空气对壁摩擦和流动扰动,压力随着速度的增加而增加。
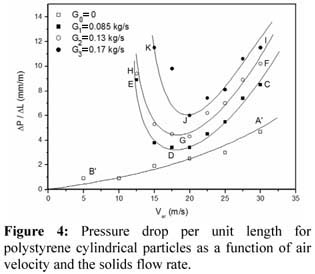
图4中的CDE部分表示固体流速为0.085kg / s(G 1 )时的压降曲线。 高风速(25米/秒)导致相对较高的压降。 随着空气速度降低并且固体质量流速保持恒定,压降达到最小点,然后由于水平管下部的固体沉降而增加。 对于所有固体流速(G 2 = 0.13kg / s和G 3 = 0.17kg / s)观察到相同的行为。
响应面法用于分析操作条件对聚苯乙烯颗粒压降的影响。 表2列出了压降的因素扰动分析。 结果显示,在99%的置信水平下,固体载荷和空气速度的二次效应(v 2 )具有统计学意义(p <0.01)。 两种操作条件对压降都有积极影响,这意味着固体载荷或空气速度的增加倾向于增加聚苯乙烯珠粒的压降。 在恒定空气速度下,总压力梯度随着固体质量流速的增加而增加。 高固体流速下的压降增加可归因于管道中较高的横截面固体浓度,从而对通过系统的空气流动产生额外的阻力。
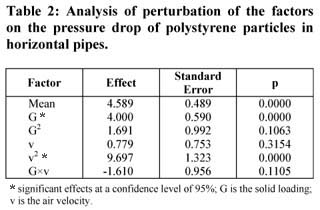
空气速度二次项的99%置信水平的正面意义表明,空气速度的增加对压降的影响远大于固体载荷。 空气速度和固体载荷之间的交叉相互作用是负的,这意味着在某些操作条件下,可以找到压降的最小值, 如图4所示 。
管道中气流的压降(G = 0)可用公式(1)表示:
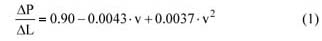
水平管道中两相流的压降(G = 0.085至G = 0.17)可用公式(2)(单位为mm / m)或公式(3)(单位为Pa / m)表示:
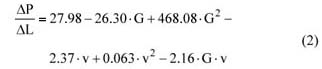
水平管道中两相流的压降(G = 0.085至G = 0.17)可用公式(2)(单位为mm / m)或公式(3)(单位为Pa / m)表示:
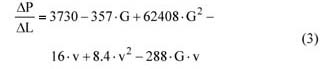
其中 ΔP/ ΔL是压降(Pa / m),G是固体流速(kg / s),v是空气流速(m / s)。
为了对任何管道直径普遍有效,可以重新定义等式(3),如公式(4)所示:
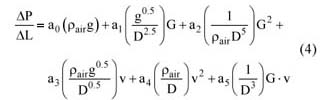
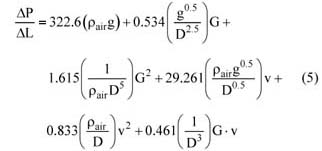
其中 ΔP/ ΔL是压降(Pa / m),D是管道直径(m),G是固体流速(kg / s),g是重力加速度(m / s 2 ) v是空气流量(m / s), ρa 是空气密度(kg / m 3 )。
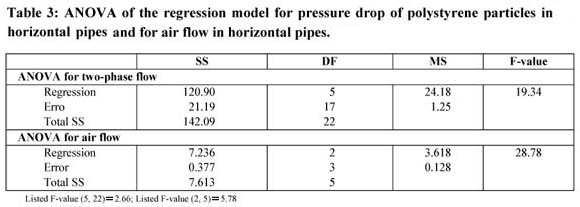
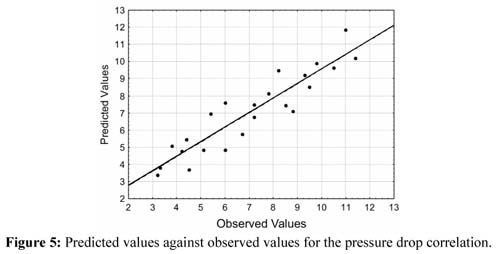
通过F检验验证了水平管中聚苯乙烯颗粒压降和水平管中气流压降的回归模型( 表3 )。 F检验的结果显示,计算的F值比列出的F值高出4倍以上(95%置信水平),表明回归模型是有效的,可用于预测水平管道中聚苯乙烯颗粒的压降。 预测值和观测值的图示于图5中 。
当空气流速很高时,固体完全悬浮在空气流中。 随着空气速度的降低,固体移动得更慢,并倾向于沉降在管道的下部。 当空气速度不足以保持所有颗粒悬浮时,颗粒开始在管道底部沉降,直到横截面完全堵塞(Rhodes,2000)。 此时,固体沿管道底部以密相输送。 这一点标志着气动输送的稀相和密相之间在水平线上的边界。
Vásquez等。 (2008)研究了4mm聚乙烯颗粒(硬颗粒和软颗粒)的压降曲线,速度在15和30m / s之间,固体载荷/空气质量在0.5和2.5之间。 Vásquez等人获得的结果。 (2008)类似于本文获得的聚苯乙烯颗粒的压降。 Vásquez等。 (2008)声称增加的压降部分是由于颗粒在通过输送系统的过程中必须多次重新加速。 另外,强烈的弹跳增加了固体和空气之间的轴向速度差异,增加了颗粒上的阻力。
Tomita和Asou(2009)研究了聚乙烯颗粒在水平管道中以非常低的速度(<8 m / s)输送。 他们观察到高压力损失,就像本研究报告的低气流速度一样,也可以通过类似于公式(3)的方程拟合。 Pahk和Klinzing(2008)对聚苯乙烯颗粒观察到相同的典型结果,但是在高空气速度和稍大的颗粒直径(3.9mm)下观察到。
水平管道中气动输送的压降也可以通过考虑气流速度,管道直径,气体密度,颗粒负载和颗粒摩擦系数的公式来拟合。 然而,颗粒摩擦系数难以计算,并且其估计存在若干相关性。 通常,颗粒摩擦系数取决于气流速度,颗粒速度,管道直径,气体密度,颗粒负荷,阻力系数,颗粒直径和气体粘度(Klinzing等,1997)。 这里提出的用于估算聚苯乙烯颗粒的水平气力输送中的压降的等式可以用作更复杂的等式的替代。
图6显示,即使远离最小压降点,也可能在管的横截面中出现不均匀的颗粒分布。 在最高风速(23 m / s)和最低固体流速(0.085 kg / s)下,固体大部分在管道底部附近运输,83%的聚苯乙烯颗粒存在于收集器中7 ,8和9( 图3 )。 在任何操作条件下,聚苯乙烯颗粒在管道中的输送不均匀分布。 当气动输送在高风速和低聚乙烯流速下运行时,发现了最佳分布。 即便如此,68%的颗粒沿管道底部移动,只有16%的颗粒被收集在管道的上层。
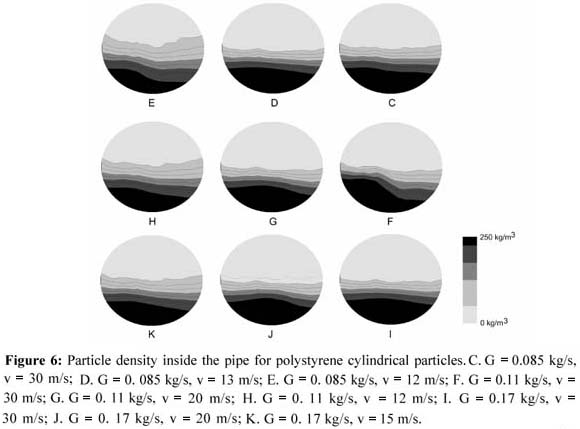
在该工作中获得的管的横截面中的颗粒分布类似于通过诸如扩展激光多普勒测速仪(LDA)的先进技术获得的水平管流的颗粒密度分布。 Lu等人。 (2009)通过使用扩展的LDA技术研究了玻璃珠的运输,并报道了类似于本文获得的颗粒分布。
这里应用的所有条件的斯托克斯数高于1,表明颗粒运动与载气流无关,因为它无法响应其变化。 对于两相流计算的最低斯托克斯数是1.53,在5m / s的空气流速下获得,其接近于颗粒的快速和慢响应时间与空气速度变化之间的理论边界。 对于两相流计算的最高斯托克斯数是10.7,在空气流速为35m / s时获得。
结果表明,作为空气速度和固体质量流量函数的压降曲线必须与管道横截面中颗粒分布的数据相结合,以加强稀相气动的设计和分析。输送系统。
聚苯乙烯在管道中的水平气动输送中呈现不均匀的颗粒分布。 圆柱形聚苯乙烯颗粒的输送主要在管的下部,即使在低固体载荷和高空气速度下也是如此。 当系统在高风速和低聚苯乙烯负载下运行时,发现了最佳分布。 结果表明研究颗粒分散和系统特征曲线的重要性
参考
Adam,O.,UntersuchungenüberdieVorgängeinfestoffbeladenenGasströmungen。 Forschungsberichte des Landes Nordrhein-Westfalen。 Westdeutscher Verlag,Köln(1960)。 [ 链接 ]
Hirota,M.,Sogo,Y.,Marutani,T。和Suzuki,M。,粉末的机械性能对斜管气力输送的影响。 Powder Tech。,122,150(2002)。 [ 链接 ]
Klinzing,GE,Marcus,RD,Rizk,F。和Leung,LS,固体气力输送:理论和实践方法。 Chapman&Hall,伦敦(1997年)。 [ 链接 ]
Kuang,SB,Chu,KW,Yu,AB,Zou,ZS和Feng,YQ,气力输送中水平段塞流的计算研究。 Ind.Eng。 化学。 Res。,47,470(2008)。 [ 链接 ]
Lain,S.,Sommerfeld,M。和Quintero,B。水平圆管中固体颗粒气力输送中二次流动的数值模拟。 布拉兹。 J. Chem。 Eng。,26,583(2009)。 [ 链接 ]
Li,H。和Tomita,Y。水平稀释旋流气力输送中的颗粒速度和浓度特性。 Powder Tech。,107,144(2000)。 [ 链接 ]
Lu,Y.,Glass,DH和Easson,WJ,通过扩展LDA技术研究气固水平管道流动中的颗粒行为。 Fuel,88,2520(2009)。 [ 链接 ]
Marcus,RD,Leung,LS和Klinzing,GE,固体气力输送:理论和实践方法。 查普曼和霍尔,纽约(1990年)。 [ 链接 ]
Molerus,O.,概述:固体的气动输送。 Powder Tech。,88,309(1996)。 [ 链接 ]
Pahk,JB和Klinzing,GE,两种不同塑料颗粒的稀相气力输送的流动特性比较。 J. Chin。 研究所。 化学。 Eng。,39,148(2008)。 [ 链接 ]
Rhodes,M。,粒子技术简介。 John Wiley&Sons,纽约(2000年)。 [ 链接 ]
Sommerfeld,M。水平通道中湍流气体 - 粒子流碰撞效应的分析:第一部分。粒子输运。 诠释。 J. Multiph。 Flow,29,675(2003)。 [ 链接 ]
Sommerfeld,M。和Lain,S。从基本过程到工业粒子流量的数值预测。 Multiph。 科学。 Tech。,21,123(2009)。 [ 链接 ]
Tomita,Y。和Asou,H。,在水平管道中低速气动输送粗颗粒。 Powder Tech。,196,14(2009)。 [ 链接 ]
Tsuji,Y。和Morikawa,Y。LDV测量水平管道中的空气 - 固体两相流。 J. Fluid Mech。,120,385(1982)。 [ 链接 ]
Tsuji,Y。和Morikawa,Y。LDV测量垂直管道中的空气 - 固体两相流。 J. Fluid Mech。,139,417(1984)。 [ 链接 ]
Vásquez,N.,Jacob,K.,Cocco,R.,Dhodapkar,S。和Klinzing,GE,粒子弹跳的可视化分析及其对稀相气力输送中压降的影响。 Powder Tech。,179,170(2008)。 [ 链接 ]
Xiong,W.,Kalkühler,K。和Merzhirch,W。,流量调节器下游的速度和湍流的测量。 In:流体计量流体力学(Ed.Merzkirch,W。),Springer,Berlin,pp.61-78(2005)。 [ 链接 ]
在塑料粒料的气力输送过程中,已经观察到具有相似物理特性的材料可能在压降方面产生显着差异。 在这项工作中,从实验角度展示了具有圆形横截面的载有颗粒的2.7米长水平通道中的压降。 对圆柱形聚苯乙烯珠粒进行实验,平均直径为3.2mm,质量载荷为0.06-0.11(kg颗粒/ kg气体)。 研究了空气质量流量在0.085kg / s至0.170kg / s的范围内。 压降曲线显示为空气速度和颗粒载荷的函数。 响应面法对空气速度,粒子载荷及其交叉关系表现出高度统计学意义。
关键词:气力输送系统; 颗粒状固体; 聚苯乙烯; 粒子分布; 压力损失。
输送管道中的固体流动通常通过应用两种不同的流动技术进行:密相和稀相。 在致密相中,施加高浓度的固体,通常大于30%v / v,速度为1-5m / s。 密相状态具有高的采集,操作和维护成本,因为它需要高气压(压力高于20 mbar / m)。 稀相输送在低于1%v / v的固体浓度和高于20m / s的速度下运行。 稀相方案成本较低,但在低运输速度下会引起不规则的管道磨损,主要是在水平管道的下部。
在稀相中气动输送系统的性能受压降的影响很大,而压降又取决于几个参数,例如材料特性,管道设计和气流。
本研究的目的是获得圆柱形聚苯乙烯颗粒的压降曲线,并分析空气速度和固体载荷对压降的影响。 响应面法用于分析空气速度和固体载荷对压降响应的影响。
材料和方法
实验装置
实验装置的圆柱形通道的总长度为4.2米。 通道的第一部分长1.5米,用于在聚合物颗粒的进料点之前获得完全发展的气流。 圆柱形通道的初始部分具有流量调节器,其位于鼓风机后0.9m处,其用于使管流中的速度分布均匀化。 流量调节器还旨在加速形成完全发展的湍流速度分布,其在调节器下游约25个直径处获得(Xiong等人,2005)。
实验装置的主要部件由圆柱形通道组成,放置在颗粒的进料点之后,长2.7米,内径117毫米。 这种配置允许建立二维流动条件,其中由于颗粒沉降,重力破坏了两相流中的圆柱对称( 图1和2 )。


通过离心式鼓风机(引持环保)引入空气,其具有100mm直径的半开式叶片,203mm直径的吸入管线和102mm方形排出部分,其连接至1Hp可变旋转马达,其中两个额外的轴承是增加(平衡鼓风机马达)来评估机械功率。
通过皮托管测量总压力和静压。 这些管由两根190mm长的“L”形同轴管组成。 内管的内径为3毫米,外管的内径为8毫米,按照ASME规范制造。 总压力通过皮托管的中心管获得,而静压通过放置在皮托管外管壁中的小孔获得。 动态压力确定为总压力和静压力之间的差值。 皮托管放置在第一个测压环后0.13米处和流量调节器后0.53米处。
在流动调节器之后,分别将第一,第二,第三和第四测压环放置在0.40米,0.60米,1.20米和3.00米处。
借助于带有六个径向叶片的旋转阀将固体从进料容器送入输送管,测量为92mm×42mm,直径为76.2mm。 将固体排放到位于水平气动输送机末端的收集器模块中。 颗粒分布分析模块由九个方形截面的铝管组成,尼龙袋连接在其上以收集固体颗粒( 图3 )。 负载 μ (固体质量流量/空气质量流量)由气流阀和旋转阀的相互作用控制。

材料
在测试中使用聚苯乙烯颗粒(PS)并由BASF提供。 聚苯乙烯颗粒的性质列于表1中 。

实验
通过将固体质量流速设定为0.085kg / s,0.13kg / s和0.17kg / s(此处分别称为G 1 ,G 2和G 3 )来建立作为空气速度的函数的聚苯乙烯压降特性曲线。 。 速度从5到35米/秒变化,载体上的压力用连接到倾斜压力计的测压环测量。 在这些条件下的最小和最大颗粒负载量分别为0.5kg颗粒/ kg空气和7.8kg颗粒/ kg空气。
聚苯乙烯在管道中的分布是根据安装在输送管末端的九管收集模块中的固体质量确定的; 管道编号如图3所示。 在每个袋中收集的质量用于计算每单位面积的质量分数,然后允许计算聚苯乙烯在管的横截面中对于所有空气速度和固体质量流速的分散。
计算九个收集器的颗粒密度,并且还使用表面响应方法处理这些点。 使用软件Statistica v7.0基于使用距离加权最小二乘法的数据内插来生成粒子分布轮廓。 应用该方法是因为它为非对称轮廓提供了更好的数据拟合。
结果与讨论
将水平和垂直方向上的压降测量值归一化为 ΔP/ L,其中L是压力抽头之间的距离。 图4显示了聚苯乙烯颗粒在水平方向上的压降与载荷和空气速度的关系。 图4中的A'B'部分表示由整个水平传输线中的空气流(无固体流速G 0 = 0)引起的压降。 由于内部摩擦,空气对壁摩擦和流动扰动,压力随着速度的增加而增加。

图4中的CDE部分表示固体流速为0.085kg / s(G 1 )时的压降曲线。 高风速(25米/秒)导致相对较高的压降。 随着空气速度降低并且固体质量流速保持恒定,压降达到最小点,然后由于水平管下部的固体沉降而增加。 对于所有固体流速(G 2 = 0.13kg / s和G 3 = 0.17kg / s)观察到相同的行为。
响应面法用于分析操作条件对聚苯乙烯颗粒压降的影响。 表2列出了压降的因素扰动分析。 结果显示,在99%的置信水平下,固体载荷和空气速度的二次效应(v 2 )具有统计学意义(p <0.01)。 两种操作条件对压降都有积极影响,这意味着固体载荷或空气速度的增加倾向于增加聚苯乙烯珠粒的压降。 在恒定空气速度下,总压力梯度随着固体质量流速的增加而增加。 高固体流速下的压降增加可归因于管道中较高的横截面固体浓度,从而对通过系统的空气流动产生额外的阻力。

空气速度二次项的99%置信水平的正面意义表明,空气速度的增加对压降的影响远大于固体载荷。 空气速度和固体载荷之间的交叉相互作用是负的,这意味着在某些操作条件下,可以找到压降的最小值, 如图4所示 。
管道中气流的压降(G = 0)可用公式(1)表示:
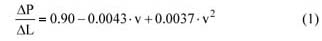
水平管道中两相流的压降(G = 0.085至G = 0.17)可用公式(2)(单位为mm / m)或公式(3)(单位为Pa / m)表示:
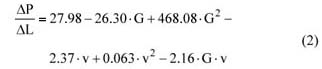
水平管道中两相流的压降(G = 0.085至G = 0.17)可用公式(2)(单位为mm / m)或公式(3)(单位为Pa / m)表示:
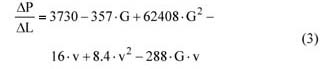
其中 ΔP/ ΔL是压降(Pa / m),G是固体流速(kg / s),v是空气流速(m / s)。
为了对任何管道直径普遍有效,可以重新定义等式(3),如公式(4)所示:
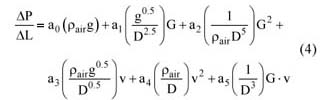
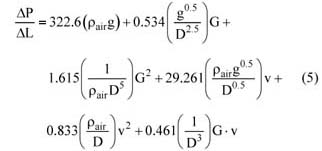
其中 ΔP/ ΔL是压降(Pa / m),D是管道直径(m),G是固体流速(kg / s),g是重力加速度(m / s 2 ) v是空气流量(m / s), ρa 是空气密度(kg / m 3 )。
通过F检验验证了水平管中聚苯乙烯颗粒压降和水平管中气流压降的回归模型( 表3 )。 F检验的结果显示,计算的F值比列出的F值高出4倍以上(95%置信水平),表明回归模型是有效的,可用于预测水平管道中聚苯乙烯颗粒的压降。 预测值和观测值的图示于图5中 。


当空气流速很高时,固体完全悬浮在空气流中。 随着空气速度的降低,固体移动得更慢,并倾向于沉降在管道的下部。 当空气速度不足以保持所有颗粒悬浮时,颗粒开始在管道底部沉降,直到横截面完全堵塞(Rhodes,2000)。 此时,固体沿管道底部以密相输送。 这一点标志着气动输送的稀相和密相之间在水平线上的边界。
Vásquez等。 (2008)研究了4mm聚乙烯颗粒(硬颗粒和软颗粒)的压降曲线,速度在15和30m / s之间,固体载荷/空气质量在0.5和2.5之间。 Vásquez等人获得的结果。 (2008)类似于本文获得的聚苯乙烯颗粒的压降。 Vásquez等。 (2008)声称增加的压降部分是由于颗粒在通过输送系统的过程中必须多次重新加速。 另外,强烈的弹跳增加了固体和空气之间的轴向速度差异,增加了颗粒上的阻力。
Tomita和Asou(2009)研究了聚乙烯颗粒在水平管道中以非常低的速度(<8 m / s)输送。 他们观察到高压力损失,就像本研究报告的低气流速度一样,也可以通过类似于公式(3)的方程拟合。 Pahk和Klinzing(2008)对聚苯乙烯颗粒观察到相同的典型结果,但是在高空气速度和稍大的颗粒直径(3.9mm)下观察到。
水平管道中气动输送的压降也可以通过考虑气流速度,管道直径,气体密度,颗粒负载和颗粒摩擦系数的公式来拟合。 然而,颗粒摩擦系数难以计算,并且其估计存在若干相关性。 通常,颗粒摩擦系数取决于气流速度,颗粒速度,管道直径,气体密度,颗粒负荷,阻力系数,颗粒直径和气体粘度(Klinzing等,1997)。 这里提出的用于估算聚苯乙烯颗粒的水平气力输送中的压降的等式可以用作更复杂的等式的替代。
图6显示,即使远离最小压降点,也可能在管的横截面中出现不均匀的颗粒分布。 在最高风速(23 m / s)和最低固体流速(0.085 kg / s)下,固体大部分在管道底部附近运输,83%的聚苯乙烯颗粒存在于收集器中7 ,8和9( 图3 )。 在任何操作条件下,聚苯乙烯颗粒在管道中的输送不均匀分布。 当气动输送在高风速和低聚乙烯流速下运行时,发现了最佳分布。 即便如此,68%的颗粒沿管道底部移动,只有16%的颗粒被收集在管道的上层。

在该工作中获得的管的横截面中的颗粒分布类似于通过诸如扩展激光多普勒测速仪(LDA)的先进技术获得的水平管流的颗粒密度分布。 Lu等人。 (2009)通过使用扩展的LDA技术研究了玻璃珠的运输,并报道了类似于本文获得的颗粒分布。
这里应用的所有条件的斯托克斯数高于1,表明颗粒运动与载气流无关,因为它无法响应其变化。 对于两相流计算的最低斯托克斯数是1.53,在5m / s的空气流速下获得,其接近于颗粒的快速和慢响应时间与空气速度变化之间的理论边界。 对于两相流计算的最高斯托克斯数是10.7,在空气流速为35m / s时获得。
结果表明,作为空气速度和固体质量流量函数的压降曲线必须与管道横截面中颗粒分布的数据相结合,以加强稀相气动的设计和分析。输送系统。
结论
聚苯乙烯在管道中的水平气动输送中呈现不均匀的颗粒分布。 圆柱形聚苯乙烯颗粒的输送主要在管的下部,即使在低固体载荷和高空气速度下也是如此。 当系统在高风速和低聚苯乙烯负载下运行时,发现了最佳分布。 结果表明研究颗粒分散和系统特征曲线的重要性
参考
Adam,O.,UntersuchungenüberdieVorgängeinfestoffbeladenenGasströmungen。 Forschungsberichte des Landes Nordrhein-Westfalen。 Westdeutscher Verlag,Köln(1960)。 [ 链接 ]
Hirota,M.,Sogo,Y.,Marutani,T。和Suzuki,M。,粉末的机械性能对斜管气力输送的影响。 Powder Tech。,122,150(2002)。 [ 链接 ]
Klinzing,GE,Marcus,RD,Rizk,F。和Leung,LS,固体气力输送:理论和实践方法。 Chapman&Hall,伦敦(1997年)。 [ 链接 ]
Kuang,SB,Chu,KW,Yu,AB,Zou,ZS和Feng,YQ,气力输送中水平段塞流的计算研究。 Ind.Eng。 化学。 Res。,47,470(2008)。 [ 链接 ]
Lain,S.,Sommerfeld,M。和Quintero,B。水平圆管中固体颗粒气力输送中二次流动的数值模拟。 布拉兹。 J. Chem。 Eng。,26,583(2009)。 [ 链接 ]
Li,H。和Tomita,Y。水平稀释旋流气力输送中的颗粒速度和浓度特性。 Powder Tech。,107,144(2000)。 [ 链接 ]
Lu,Y.,Glass,DH和Easson,WJ,通过扩展LDA技术研究气固水平管道流动中的颗粒行为。 Fuel,88,2520(2009)。 [ 链接 ]
Marcus,RD,Leung,LS和Klinzing,GE,固体气力输送:理论和实践方法。 查普曼和霍尔,纽约(1990年)。 [ 链接 ]
Molerus,O.,概述:固体的气动输送。 Powder Tech。,88,309(1996)。 [ 链接 ]
Pahk,JB和Klinzing,GE,两种不同塑料颗粒的稀相气力输送的流动特性比较。 J. Chin。 研究所。 化学。 Eng。,39,148(2008)。 [ 链接 ]
Rhodes,M。,粒子技术简介。 John Wiley&Sons,纽约(2000年)。 [ 链接 ]
Sommerfeld,M。水平通道中湍流气体 - 粒子流碰撞效应的分析:第一部分。粒子输运。 诠释。 J. Multiph。 Flow,29,675(2003)。 [ 链接 ]
Sommerfeld,M。和Lain,S。从基本过程到工业粒子流量的数值预测。 Multiph。 科学。 Tech。,21,123(2009)。 [ 链接 ]
Tomita,Y。和Asou,H。,在水平管道中低速气动输送粗颗粒。 Powder Tech。,196,14(2009)。 [ 链接 ]
Tsuji,Y。和Morikawa,Y。LDV测量水平管道中的空气 - 固体两相流。 J. Fluid Mech。,120,385(1982)。 [ 链接 ]
Tsuji,Y。和Morikawa,Y。LDV测量垂直管道中的空气 - 固体两相流。 J. Fluid Mech。,139,417(1984)。 [ 链接 ]
Vásquez,N.,Jacob,K.,Cocco,R.,Dhodapkar,S。和Klinzing,GE,粒子弹跳的可视化分析及其对稀相气力输送中压降的影响。 Powder Tech。,179,170(2008)。 [ 链接 ]
Xiong,W.,Kalkühler,K。和Merzhirch,W。,流量调节器下游的速度和湍流的测量。 In:流体计量流体力学(Ed.Merzkirch,W。),Springer,Berlin,pp.61-78(2005)。 [ 链接 ]
- 上一篇:你知道稀相真空气力输送系统嘛?
- 下一篇:气力输送工程现场照片